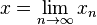Eksponen adalah perkalian yang diulang-ulang. Orang menulis eksponen dengan indeks di atas, yang akan terlihat sebagai berikut:  . Terkadang hal itu tak mungkin. Kemudian orang menulis eksponen menggunakan tanda ^: 2^3 berarti
. Terkadang hal itu tak mungkin. Kemudian orang menulis eksponen menggunakan tanda ^: 2^3 berarti 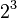 .
.
Bilangan  disebut bilangan pokok, dan bilangan
disebut bilangan pokok, dan bilangan  disebut eksponen. Sebagai contoh, pada
disebut eksponen. Sebagai contoh, pada 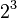 , 2 adalah bilangan pokok dan 3 eksponen.
, 2 adalah bilangan pokok dan 3 eksponen.
Untuk menghitung 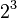 seseorang harus mengalikan 3 kali terhadap angka 2. Sehingga
seseorang harus mengalikan 3 kali terhadap angka 2. Sehingga  . Hasilnya adalah
. Hasilnya adalah  . Apa yang dikatakan persamaan bisa juga dikatakan dengan cara ini: 2 pangkat 3 sama dengan 8.
. Apa yang dikatakan persamaan bisa juga dikatakan dengan cara ini: 2 pangkat 3 sama dengan 8.
Contoh:
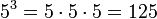

-
 untuk setiap bilangan x
untuk setiap bilangan x
Jika eksponen sama dengan 2, maka disebut persegi karena area persegi dihitung menggunakan 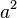 . Sehingga
. Sehingga
-
 adalah persegi dari
adalah persegi dari 
Jika eksponen sama dengan 3, maka disebut kubik karena volume kubus dihitung dengan 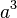 . Sehingga
. Sehingga
-
 adalah kubik
adalah kubik 
Jika eksponen sama dengan -1 orang harus menghitung inversi bilangan pokok. Sehingga: Jika eksponen adalah integral dan kurang dari 0, orang harus membalik bilangan dan menghitung pangkat. Sebagai contoh:
Jika eksponen adalah integral dan kurang dari 0, orang harus membalik bilangan dan menghitung pangkat. Sebagai contoh:
Jika eksponen sama dengan  hasilnya adalah akar persegi bilangan pokok. Sehingga
hasilnya adalah akar persegi bilangan pokok. Sehingga  Contoh:
Contoh:
Dengan cara yang sama, jika eksponen  hasilnya adalah akar ke-n, sehingga:
hasilnya adalah akar ke-n, sehingga:
Jika eksponen merupakan bilangan rasional  , hasilnya adalah akar ke-q bilangan pokok yang dipangkatkan p, sehingga:
, hasilnya adalah akar ke-q bilangan pokok yang dipangkatkan p, sehingga:
Eksponen bisa juga tak rasional. Untuk menjadikan bilangan pokok a menjadi pangkat ke-x yang tak rasional, kita menggunakan rangkaian ketidakterhinggaan bilangan rasional (xi), yang limitnya adalah x:
seperti ini:
Ada beberapa aturan yang membantu menghitung pangkat:





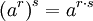
-
 : Bila bilangan pokok lebih besar daripada 1 dan eksponen 0, jawabannya 1. Jika bilangan pokok dan pangkat sama dengan 0, jawabannya tak terdefinisikan.
: Bila bilangan pokok lebih besar daripada 1 dan eksponen 0, jawabannya 1. Jika bilangan pokok dan pangkat sama dengan 0, jawabannya tak terdefinisikan.
Ekponen matriks bisa pula dihitung. Matriks itu harus persegi. Sebagai contoh:  .
.
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.
Rumus dasar logaritma:
bc= a ditulis sebagai blog a = c (b disebut basis)
Beberapa orang menuliskan blog a = c sebagai logba = c.
Sumber : http://id.wikipedia.org/wiki/Logaritma



![a^{\frac{1}{n}}=\sqrt[n]{a}](http://upload.wikimedia.org/math/c/d/e/cde604330dc8b9bb773376cb1fbf2098.png)
![a^{\frac{p}{q}}=\sqrt[q]{a^p}](http://upload.wikimedia.org/math/d/1/6/d16207859e88dd632865a3019610698c.png)